Cheesing Kepler's Laws for better performance
Our team has been doing game jams together for a while now, but this it the first time we are using Godot together. For previous jams I was always very worried about making sure that all of our code and assets were in sync. I was pleasantly surprised that Godot's signal system made our disparate sets of code very easy to integrate: we could work on different parts of the project separately without coordinating too much, and piece it together at the end without too much trouble. I definitely think we should keep using this engine going forward.
Another feature I adore about Godot is the ability to make scripts modify the behavior of the editor. Our game features a complicated tree of solar systems orbiting a black hole, each with several planets and moons. Each celestial body needed a different gravitational field, and orbital paths dictated by Kepler's laws. We wrote a scene in Godot that let us rearrange the planets and their orbits with drag and drop, which automatically drew the paths of the orbits in the editor just as it does in game. To tune the strength of the gravity, we drew a vector field that indicated the acceleration a test mass would experience if it were at that position. Calculating that vector field for the entire scene is way too expensive, so we added a rectangle shape that dictates where that vector field is drawn. A convenient visual editor for designing solar systems let us design a bigger and more interesting game.
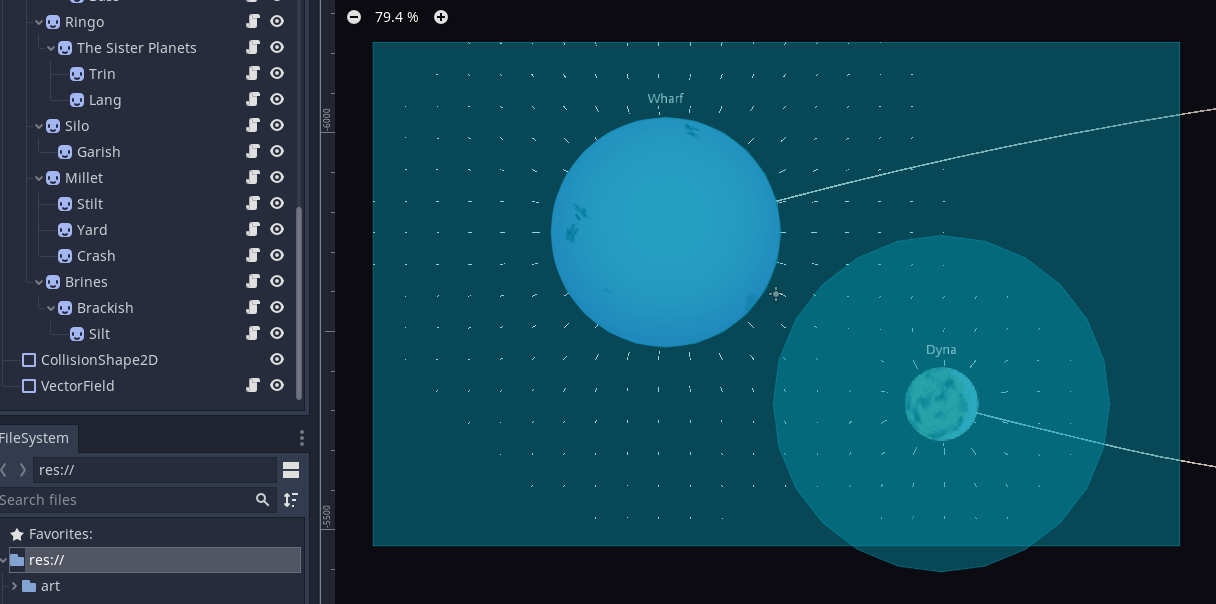
Above: drawing planetary movement, as well as a vector field to indicate gravitational strength in the Godot editor.
An initial draft of this game involved simulated gravity between all celestial bodies. Amazingly, this performed pretty well! The problem was that the orbits got pretty wonky, as the gravity of planets was strong enough to affect the orbits of other planets. So we opted to put the planets on rails: to fix their orbit into a particular ellipse as determined by Kepler's laws. Only the Ship's movement is determined through numerical integration.
However, it turns out that Kepler's laws are actually rather expensive to compute directly! The radius-as-a-function-of-angle function is simple enough. The problem is the angle-as-a-function-of-time function, which requires solving a minimization using the Newton-Raphson method. No way we are doing that for every planet for every frame. So instead, I found a different timing function that is easy to compute, and still replicates the approximate behavior of Kepler's second law: slow near apoapsis, fast near periapsis.
Files
Orbits
Simulation of a ship soaring through the universe near suns and planets. Branching dialogue stories are there to find.
| Status | Released |
| Authors | the_nope_slope, powercactus, cousday, AustereTriceratops |
| Genre | Simulation, Interactive Fiction, Visual Novel |
| Tags | 2D, Exploration, Narrative, Physics, Space |
More posts
- Data Driven Quest System with JSONMar 20, 2022
- Art and StoryMar 20, 2022
Leave a comment
Log in with itch.io to leave a comment.